"The Laws of General Relativity " do not take into account the Refraction of Light.
Thus, the occurences of redshift, lensing, and time dilation actually can be explained in conjunction with the refraction of light,
The effect of refraction: tume delay of light.An example the Sunlight, A-B a little bit longer than A'-B
The apparent position of an object in the sky may be
changed by several different physical effects.
One of these is
refraction.
The speed of light changes as it passes through a
medium such as air.
We define the refractive index of any
transparent medium as 1/v,
where v is the speed of light in that
medium.
The speed of light in air depends on its temperature
and its pressure,
so the refractive index of the air varies in
different parts of the atmosphere.
Make a simple model of the atmosphere as n
layers of uniform air above a flat Earth,
with a different
velocity of light vi for
each layer (i from 1 to n).
Apply Snell's Law of
Refraction at each boundary.
 At
the first boundary, sin(i1) / sin(r1) = v0
/ v1 .
At
the first boundary, sin(i1) / sin(r1) = v0
/ v1 .
At the next boundary, sin(i2)
/ sin(r2) = v1 / v2 , and so on.
But, by simple geometry, r1 = i2,
r2 = i3 and so on.
So we have
sin(i1) = (v0 /
v1) sin(r1)
=
(v0 / v1) sin(i2)
=
(v0 / v1) (v1 / v2)
sin(r2)
=
(v0 / v2) sin(r2)
=
..........
=
(v0 / vn) sin(rn)
In other words, the refractive indices of the
intervening layers all cancel out.
The only thing that matters is
the ratio between v0
(which
is c, the speed of light in vacuum)
and vn (the
speed in the air at ground level).
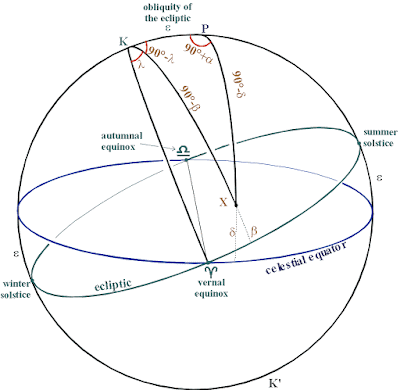
Now rn is the apparent zenith
distance of the star, z',
and i1 is its true zenith
distance, z.
So sin(z) = (v0 / vn)
sin(z').
Refraction has no effect if a star is at the zenith
(z=0).
But at any other position, the star is apparently raised;
the effect is greatest at the horizon.
Define the angle of refraction R by R = z -
z'.
Rearrange this as z = R + z'.
Then sin(z) = sin(R)
cos(z') + cos(R) sin(z').
We assume R will be small, so, approximately,
sin(R)
= R (in radians), and cos(R) = 0.
Thus, approximately,
sin(z)
= sin(z') + R cos(z').
Divide throughout by sin(z') to get
sin(z)/sin(z') = 1 + R/tan(z')
which is to say,
v0/vn
= 1 + R/tan(z').
So we can write
R
= (v0/vn - 1) tan(z')
We write this
as
R = k tan(z')
where
k = (v0/vn - 1)
Here v0 is c, the velocity of light in a
vacuum, which is constant.
But vn depends on
the temperature and pressure of the air at ground level.
At
"standard" temperature (0°C = 273K) and pressure (1000
millibars),
k = 59.6 arc-seconds.
The formula in the Astronomical Almanac is
k
= 16.27" P/(273+T)
where P is in millibars, and T is in °C.
( www.st-and.ac.uk )
Atmospheric extinction is the reason that the best spot in the sky to observe astronomical objects is the
zenith
which is directly overhead. Star light travels through less atmosphere
at the zenith than in any other direction. Extinction is worst at or
near the horizon.
For example, you can look directly at a Sun set because the Sun's
light has maximum atmospheric absorption at the horizon. When the Sun
is high in the sky it is painful and
 dangerous
dangerous to look at the
Sun without optical protection.
Refraction does make a star appear higher
in the sky
than it actually is.
Refraction
As stellar light passes through the atmosphere, it is
refracted
(bent) just as through a lens. This bending results from the increase
in the atmosphere’s density as the light ray travels downward
toward the observer. Thus refraction makes an object appear higher in
the sky than it actually is.
( www.ngawhetu.com )
( www.solarplots.info )
Light is all around us, from both natural and artificial sources, during
the day and the night. We think we understand it, and that what we see
by it is an exact representation of what we are looking at. However we
can be mistaken; the setting sun seen on the horizon has in fact already
dropped below the horizon. Twinkling stars are also an effect of this
same process, called refraction.
Light passing through a medium such as air or water can be absorbed and
scattered by the molecules in the medium or refracted by changes in air
density. Earth's atmosphere contains air, water and dust molecules that
cause light rays from the sun to change direction as they pass through
slightly different densities of air - this is known as refraction.
The
amount of refraction of light is dependent on the refractive index (a
measure of how much a substance bends light, dependent on its density
and the type of molecules) and the incident angle at which the light
enters the substance. Denser substances such as water will bend the
light more than a less dense substance like air, and light entering a
substance at an angle will refract more than entering perpendicular to
the substance's surface. Air itself can have different indices- air that
is warm will be less dense and so will refract light less.
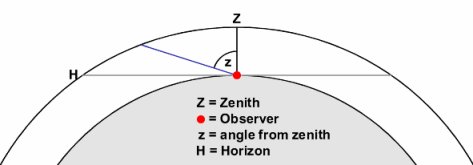
Looking up in the direction of the zenith, an observer will look through
one air mass- ie the minimum amount of air that light from the sun will
travel through to the surface.
Light at an angle z from the zenith will
pass through more air, so travels through an equivalently greater air
mass at a greater incidence angle z. Roughly, the air mass varies with
secant z,
as
cos(z)=1 airmass / n airmasses in a first-order case,
although for large angles (for more than about 60 degrees) away from the
zenith, this is less accurate due to the spherical nature of the
atmosphere.
At the horizon, light will travel through a maximum of about
38 air masses to reach an observer at sea level.
However if the observer is above sea level, for example on a
mountain or in a plane, the air mass can be greater than 38, due to the
line-of-sight passing through more air before reaching the observer's
horizon.
This change in air mass depending on where an observer looks in the sky
changes the amount and type of light reaching the observer's position.
Rayleigh (1871) found that the probability of a single photon (or packet
of light energy) being scattered by an air molecule was inversely
proportional to its wavelength to the fourth power.
Blue light with a
wavelength of about 450nm has more chance of being scattered than red
light at 660nm. Light (especially the blue end of the spectrum)
travelling through a greater air mass will be scattered more as there is
more chance of encountering particles over this larger volume in the
line-of-sight. The consequences of this are that the sun (as a single
source) appears dimmer and redder near the horizon than from the zenith,
as more light, especially bluer light, is scattered out of the
line-of-sight to the observer.
At zenith the sun's light is not
scattered as much and so only a little blue light is lost- the sun
appears white or slightly yellow. Conversely skylight (light from the
sun scattered onto air and water molecules and so arriving at the
observer from a direction other than the sun) looks bluer as it is
mostly the blue light that is scattered in all directions that reaches
the observer.
Viewing Astronomical Objects
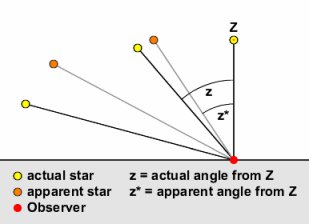
The
light from stars and other objects such as the sun, moon and planets is
also subject to these refractive properties which can cause the objects
to appear higher in the sky than they actually are.
Again, light from stars near the horizon passes through a larger volume
of air at a larger incidence angle than near the zenith, therefore
encountering more changes in air density and so refracts more. The
observer's eyes see the star where the light appears to be coming from,
not the origin of the convoluted path that it actually takes. The closer
to the horizon the star is, the greater amount of refraction we see and
the greater disparity in apparent position.
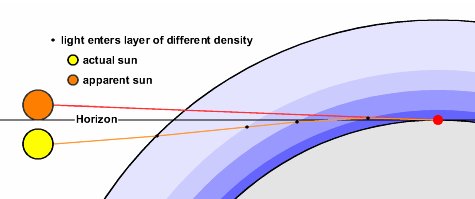
Consequently the sun or any celestial object setting on the horizon will
be refracted the largest amount. As mentioned before, the angle of
refraction is great enough that an observer can see the sun when it is
actually below the horizon. The disk of the sun has an angular distance
of about 30 arcminutes (or half a degree).
The index of refraction for
dry air at sea level is about 1.0002941, which means that the amount of
refraction in dry air is also quite small - about 39 arcmins, but enough
that as the bottom of the sun's disk is seen to touch the horizon, the
top is actually 9 arcmins below the horizon.
Twinkling Stars
Refraction also occurs with small variations in air density due to
uneven heating of the air (characterized by increased winds). This leads
to small amounts of refraction of a star's light that an observer sees
as twinkling (also known as scintillation). Again as the star's light
travels through greater air mass near the horizon, the greatest
twinkling is seen at the horizon.
Two processes occur
when looking at a star: light is momentarily refracted so as to appear
to come from a slightly different position, and light is scattered in
different directions, so decreasing the amount of light from the star
that reaches the observer. These processes cause the star to appear to
deviate slightly from its position, and to fade for split seconds of
time, causing the star to twinkle.
Stars very near the horizon can also be seen to change colour
momentarily. This is due to the light of different wavelengths (or
colours) being dispersed different amounts by slight changes in the air.
The star can appear any colour of the spectrum as the observer either
sees the bluer light that is refracted or the redder light that is left
or any colour in between before changing quickly again.
Objects with a measurable angular size such as the moon and planets
do not appear to twinkle- this is due to the fact that light from the
object is reaching the observer from all points on the object's disk. If
one light ray is refracted out of line-of-sight, it does not make a
noticeable difference to the observer, and light from the whole disk can
not be deflected at the same time. There is also a chance that light
from another point on the disk would be refracted into the line-of-sight
so the intensity of light would not change.
An observer, therefore, can only be sure that what he is looking at is a
true representation of an object if he is looking straight up to the
zenith. Any view towards the horizon will be subject to increasing
refractive and scattering effects, that can cause disparity in an
object's position, changes in the colour of the incoming light and
minute changes in the quality of light causing twinkling.
( www.math.ubc.ca )
Snell's Law
Snell's law states that the ratio of the sines of the angles of incidence and refraction is equivalent to the ratio of phase velocities in the two media, or equivalent to the reciprocal of the ratio of the indices of refraction:
with each
0 as the angle measured from the normal of the boundary,
v as the velocity of light in the respective medium (SI units are meters per second, or m/s) and
n as the refractive index (which is unitless) of the respective medium. (
Snell's Law ).
If Einstein's theory of relativity was correct, then the light from
stars that passed closest to the sun would show the greatest degree of
"bending." ( undsci.berkeley.edu )
Gambar ilustrasi di atas sebenarnya kurang cermat
Sesuai gambar di atas, jika teori relativitas umum benar, maka :
1. Cahaya
dari bintang-bintang yang berlalu dekat dengan medan gravitasi matahari
akan menunjukkan tingkat terbesar pembelokannya.
2. Semakin jauh dari
medan gravitasi matahari, sudut penyimpangannya akan semakin kecil.
3. Dan ketika cahaya bintang-bintang itu bebas dari medan gravitasi
matahari, maka tidak ada perbedaan antara posisi sejati dan posisi semu
bintang.
Dari gambar dan penjelasan di atas dapat diartikan, ketika malam hari
cahaya bintang-bintang bebas dari medan gravitasi matahari, maka tidak
ada perbedaan antara posisi sejati dan posisi semu bintang.
Hal tersebut di atas adalah sesuatu yang tidak
mungkin. Gambar di atas bisa menjelaskan bahwa hipotesis cahaya membelok di medan gravitasi benda masif, adalah tidak benar alias keliru. Benda-benda angkasa atau bintang-bintang yang dilihat oleh para mengamat, baik
dengan menggunakan alat maupun melihatnya dengan mata telanjang,
semuanya menunjukkan posisi semu ( observed / apparent position ) dan
bukan posisi sejatinya ( actual / true position ). Pembelokan cahaya bukan disebabkan karena gravitasi, melainkan karena adanya refraksi sinar ( refraction ). Sudut pembelokan bisa dihitung dengan menggunakan Hukum Snellius ( Snell's Law ).
Catatan :
Gambar ilustrasi dari undsci.berkeley.edu di atas bisa digunakan untuk
menjelaskan kekeliruan hipotesis Enstein, namun gambar ilustrasi itu
sendiri sebenarnya kurang cermat. Observed / apparent position of star
selalu tampak oleh penilik di bumi lebih tinggi dari true / actual
position.
The effect of astronomical refraction is to make a celestial body appear higher in the sky than it otherwise would.
Sehingga penggambaran di slide yang digunakan untuk
pengajaran astronomi, apparent position harus diletakkan di atas actual position.
Sehingga urut-urutan gambar di atas seharusnya matahari digambar agak
ke bawah, lalu diatasnya gambar no.1, no.2,dan no.3 masing-masing dengan
posisi apparent position di atas actual position.
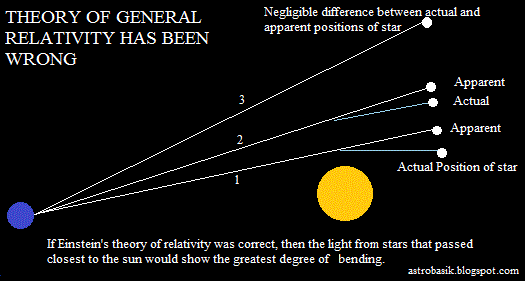
Gambar ilustrasi yang benar apparent position selalu lebih tinggi dari actual position of star.
Di bawah ini bukti tertulis bahwa Einstein mengabaikan pembiasan cahaya/refraction:
"Einstein proposed therefore, that photographs be taken of the stars immediately bordering the darkened face of the sun during an eclipse and compared with photographs of those same stars made at another time."(Lincoln Barnett, The Universe and Dr. Einstein, London, June 1949, Preface by Albert Einstein Himself, page 78 ).
Cara pembuktian di atas - dengan menggunakan fotografi - berarti mengabaikan pembiasan cahaya/refraction dan juga mengabaikan bulatan angkasa/celestial sphere. Masing-masing tempat di bumi memiliki celestial sphere sendiri, oleh karenanya foto bintang dari suatu kota tidak bisa dibandingkan dengan foto bintang yang sama, yang diambil dari kota lain. Hal ini sepertinya tidak dipahami oleh Einstein yang dengan mudahnya membandingkan foto-foto bintang, lebih-lebih lagi foto-foto tersebut diambil pada waktu yang berlainan, menganggap seakan-akan bintang-bintang itu bukan suatu obyek yang bergerak.